 For the latest deconvolution results, click here. For the latest deconvolution results, click here.
Comparison of Biaram 2-D Deconvolution Methods for Correction of Gaussian Blur
Unlike out-of-focus blur, Gaussian blur does not have strong high frequency components in the PSF so it is more difficult to recover high frequency detail by deconvolution. These experiments use a tiny input image (36x30 pixels) blurred in the computer by a 9x9 pixel Gaussian PSF. No noise was added. The object of these tests is not to demonstrate the effectiveness of the algorithms on real-world data (for that see the clock blur example). Rather it allows many iterations to be performed to assess the restoration capabilities of the various methods when taken to the limit.
All results are shown for 16777216 iterations (it takes about 3 days to run two such deconvolutions simultaneously on a hyperthreaded 3.06GHz Pentium 4 PC). The results of two novel algorithms I am developing are also shown (these are not yet released in the public distribution). After the pictorial results are presented, a comparative graph is shown giving quantitative results in the form of residual statistics (explained below). Although no noise is added there is the inevitable quantisation error which becomes significant with Gaussian blur recovery and is a challenge to any method.
16.03.2008
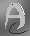

|
The original test card image and its Power spectrum
This synthetic image has a smooth sinusoidally varying background with high frequency freatures in the foreground. Note especially the dark and light isolated pixels and the narrow gap between the top right of the 'A' and the highlight streak. These are particularly difficult features to recover after a Gaussian-type blur |
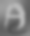

|
The blurred testcard and its power spectrum
This image forms the input to the algorithms. It is the testcard blurred by a 9x9 pixel Gaussian. The image boundaries were treated by mirror reflection geometry. Download the double preceision FITS images and Van Cittert settings file below if you want to attempt to reproduce these results (these images are copyright of Dr P. J. Tadrous and may not be published without his written permission):
 Blurred image. Blurred image.
 PSF. PSF.
 Settings file. Settings file.
|
|
Truth
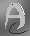

|
Deconvolved
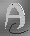

|
Input
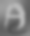

|
New Method 1
This new method is non-linear. It searches for an optimal solution in terms of local goodness of fit. It gives the best results of all the methods shown with good recovery of high spatial frequencies. The full properties of this new method are not yet known. You can see an amination of this method on the research index page of this website (JavaScript must be enabled). This shows the results of successive interation intervals going up in powers of 2 from 0 to 16.7 million.
|
|
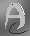

|
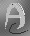

|
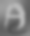

|
Van Cittert
This gives the best results of all the conventional methods (better than maximum entropy and Lucy-Richardson, etc). Compare this situation to the clock blur page where Van Cittert is not useful. This emphasises that the algorithm should be taylored to the application and that no one algorithm should be seen as a 'cure-all'.
|
|
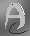

|
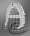

|
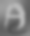

|
New Method 2
This is the second of my novel algorithms which works using a geometrical transformation model and is applicable in hardware as a parrallel process so is potentially a real-time deconvolution algorithm. It gives similar results to maximum entropy methods.
|
|
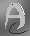

|
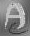

|
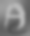

|
Maximum Entropy
(Gull and Daniel)
The results show moderate recovery of detail with lack of high frequency restoration as illustrated in the power spectrum. Gamma = 0.0123. |
|
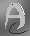

|
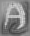

|
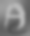

|
Maximum Entropy
(Myrheim and Rue)
The results show a moderate restoration with lack of fine detail. The power spectrum shows only partial recovery of higher spatial frequencies (not quite as good as the Gull and Daniell method).
The algorithm used an estimated noise variance of 5.0e-6. |
|
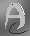

|
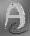

|
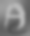

|
Lucy-Richardson
This gives a comparable result to Gull and Daniell maximum entropy (a slightly better restoration than the Myrheim & Rue algorithm). |
|
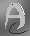

|
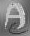

|
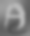

|
Super-Resolution
This gives results that are similar to Lucy-Richardson. |
|
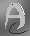

|
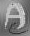

|
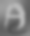

|
Landweber
I have found Landweber to be a robust method giving good results in most circumstances. Although not the best method in this test, the results are stable and respectable and, as discussed below, the result was still converging even at the 16.7 millionth iterate. |
|
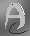

|

|

|
Least Squares
Gamma = 1e-06. Antireflective boundary treatment was required to prevent excessive boundary artefacts. This is a one-step non-iterative mothod so is very quick (this result only took a matter of seconds). |
Quantitative Results
|
|
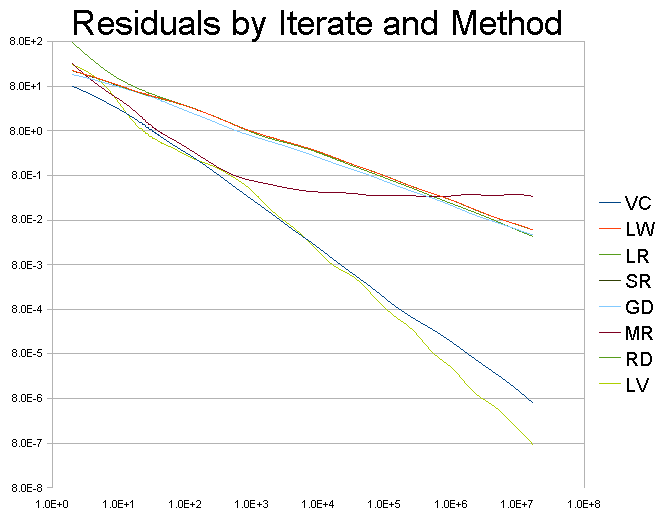
These are log-log scale plots of 'Residual' (on the ordinate) vs. 'Iteration' (abscissa) for each of the iterative methods: VC = van Cittert, LW = Landweber, LR = Lucy-Richardson, SR = Super-Resolution, GD = Gull & Daniell, MR = Myrheim & Rue, RD = New method 2, LV = New method 1.
The Residual is calculated by convolving the estimate of the solution (at the current iteration) with the PSF, then calculating the integral of the absolute difference between this image and the input image. a 5 pixel rim all around the image is ignored in this integration so as not to bias the result due to the various boundary artefacts that my occurr with any of the methods. If the restoration is perfect then this residual should be zero. The closer to zero it is the better the estimate (the deconvolution results are all constrained to be non-negative).
These cueves indicate that the 'New Method 1' (i.e. LV) gives the best final restoration of all the methods (lowest residual). The convergence rate, in terms of improvement per iteration, is variable (perhaps to be expected of a non-linear method). This rate is also comparable to the VC method which is better than all the other methods. However, this new method (LV) surprisingly diverges from the VC rate as iterations progress to give an even faster rate of convergence with increasing iterations compared to VC. As the method generally restores the lower frequencies first with further iterations refining the high freqency detail (see the animation on the research index page), this indicates that it gives a 'faster' rate of improvement of high frequency detail than all the other methods tested. It should be appreciated that this 'speed' is in terms of improvement per iteration not actual speed of calculation as this method actually takes about twice as long to calculate each iteration compared to a typical Van Cittert iteration (i.e. there are more calculations per iteration).
Van Cittert appears to give the next best restoration in terms of convergence and final restoration residual.
While the MR method of maximum entropy gives steeper convergence than all but the LV method early on, the solution quickly converges to the 'best achievable' for this algorithm and then oscillates about this point without improvement despite further iterations. My understanding is that this 'best' estimate is limited partly by the estimate of the noise variance and a lower noise variance estimate should result in a more detailed final restoration but I was unable to run the algorithm with a lower noise estimate that that used here without running into numerical exception errors. This may be a problem with my implementation rather than the algorithm itself.
The other methods (LW, LR, SR, RD, GD) are very similar to each other in terms of rate of convergence and quality of the final estimate.
With the sole exception of the MR method, all the other solutions appear to be continuing to improve with increasing iterations at the time the experiment was stopped. This suggests that further iterations may result in further improvement in the solution. However, as this is a log-log graph, the improvement is asymptotic so it is impractical to obtain significant improvement.
|
|

 For the latest deconvolution results, click here.
For the latest deconvolution results, click here.







 Blurred image
Blurred image

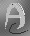

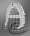

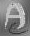

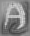






 Dr P. J. Tadrous 2000-2024
Dr P. J. Tadrous 2000-2024